Situation déclenchante

 Problématique

Y a-t-il des leaders sur les réseaux sociaux ?

 Travail à faire

Télécharger le formulaire de réponse en cliquant sur le lien pdf ci-dessous, le compléter au fur et à mesure de l'activité et le rendre en ligne via le Travail à Faire > Rendre

Réseau de type Facebook

Inspiré de l’activité de Philippe Letenneur et Philippe Morin - Académie de CAEN

Alban, Béatrice, Charles, Déborah, Éric, Fatima et Gérald, sont inscrits sur Facebook :

• Alban est ami avec Béatrice, Éric et Fatima.
• Béatrice est amie avec Alban, Charles, Déborah.
• Charles, lui, est ami avec Béatrice, Déborah et Gérald.
• Déborah est amie avec Béatrice, Charles et Gérald.
• Éric, avec Fatima et Alban.
• Fatima, avec Alban Éric.
• Gérald, avec Charles et Déborah

1 - Qui a le plus d'amis ? Le moins ?    

2 - Tous les participants ont-ils des amis en commun ?    

3 - Peuvent-ils tous entrer en contact par le biais de leurs amis ?

4 - La description ci-dessus est peu explicite alors que ce réseau social ne regroupe que 7 abonnés. Imaginer une description pour une centaine d’abonnés ! On peut donc représenter ce réseau avec un tableau à 2 entrées dans lequel il suffit de faire une croix dans chaque case pour modéliser les relations d’amitié (à compléter dans la colonne de gauche). Compléter la fiche travail.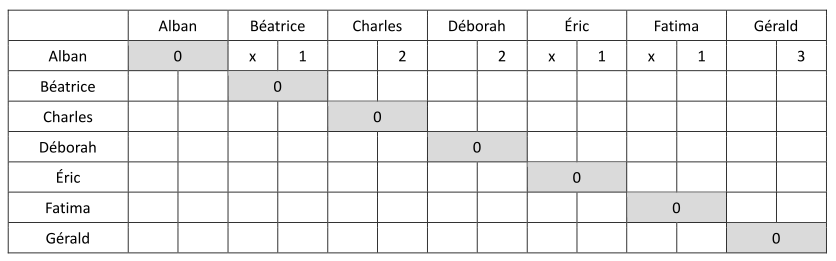

5 - On peut aussi représenter ces relations d’amitié avec un graphe :

• Chaque abonné est représenté par un cercle bien identifié qu’on appelle sommet.
• Chaque relation d’amitié entre abonnés est représentée par un segment reliant deux sommets.
• Ce graphe représente des relations non orientées : on considère que si Alban est ami avec Béatrice, celle-ci est aussi amie avec Alban. Dans ce cas, la relation est représentée par un trait rectiligne, c’est une arête.

Compléter le graphe sur la fiche travail :

La distance entre deux sommets est le nombre minimum d’arêtes qu’il faut parcourir pour aller d’un sommet à un autre.

6 - Complète le tableau précédent avec la distance entre chacun des sommets du graphe (colonne de droite).

L’écartement d’un sommet est la distance maximum entre ce sommet et les autres sommets.

7 - Remplir le tableau sur la fiche travail.

8 - Le diamètre d’un graphe est la distance max entre 2 sommets de ce graphe. Déterminer le diamètre de ce graphe.

9 - Le centre d’un graphe est l’ensemble des sommets d’écartement minimal. Déterminer le centre de ce graphe.

10 - Le rayon d’un graphe est l’écartement d’un des sommets du centre du graphe. Déterminer le rayon de ce graphe.

Réseau de type X

La représentation est différente dans le cas d’un réseau comme celui créé par Twitter : Éric peut être un « follower » à Déborah sans que la réciproque soit nécessairement vraie. Dans ce cas, la relation est dite orientée. Elle est alors représentée par une flèche.

Plus de Tutos Graph Online : https://graphonline.ru/en/help

12 - Quel est le diamètre de ce graphe ? son centre ? son rayon ?

13 - Qui sont les leaders de ces 2 réseaux sociaux ?  

14 - Pour qui cette information est-elle intéressante et pourquoi ?

Traitement des données par programmation

15 - À partir de l’exemple ci-dessous réaliser le programme du réseau de type facebook étudié plus haut.

Le programme permettra de...

• Tracer le graphe et l’exporter au format .pdf

• Donner les informations suivantes :  

• Nb de sommet

• Nb d’arêtes

• Diamètre du graphe

• Rayon du graphe

• Centre du graphe

Accès à l'activité avec   

Attention : pour programmer une relation non orientée, il est nécessaire de créer 2 arêtes

16 - Quel intérêt présente ici la programmation pour traiter les données ? 

17 - Comment les entreprises des réseaux sociaux doivent-ils l’utiliser ?     

Le "petit monde" de Milgram et le "petit monde" des réseaux sociaux

18 – Qu’est-ce que le petit monde de Milgram est quel est l’impact des réseaux sociaux ?

Les algorithmes dans les réseaux sociaux

19 – Quel est le risque des algorithmes dans les réseaux sociaux appelé "bulle de filtre" ?